We see that you have published the source code,
but wefre having trouble deciphering the mathematical model and governing equations of the system. Specifically,
many of the variable explanations get lost in translation.
We were wondering if you would be comfortable sharing any labeled models or equations that you used for this project.
A.1
Currently, I am in the stage of verifying the mechanical image by physics simulation.
They have demonstrated the effectiveness of UVC, but a clear mathematical model has not yet been constructed.
I hope that other research institutes will pursue the mathematical model of UVC.
Also, since it is in the experimental stage and trial and error is repeated, the comments on variables etc. are very rough.
Q.2
We attempted to model your joint lengths and angles,
but failed to understand angle k (K0GÈ°px) and angle x (K0rUèpx).
Are these approximations or is there something that we are perhaps misunderstanding?
A.2
@ There was an error in the calculation of xiK0rUèpxj.
x=asin(x/LEG)@Ë@x = asin(x/k)
A Another. There was a discrepancy between the ODE object settings and the parameter settings.
#define LEG 190.0@Ë@#define LEG 180.0
It doesn't matter so much in operation,
but it is mathematically inconsistent, so I fixed it.
Updated core.cpp.
Please refer to the following memo for the explanation about the calculation of the hip joint angle and the knee joint angle.
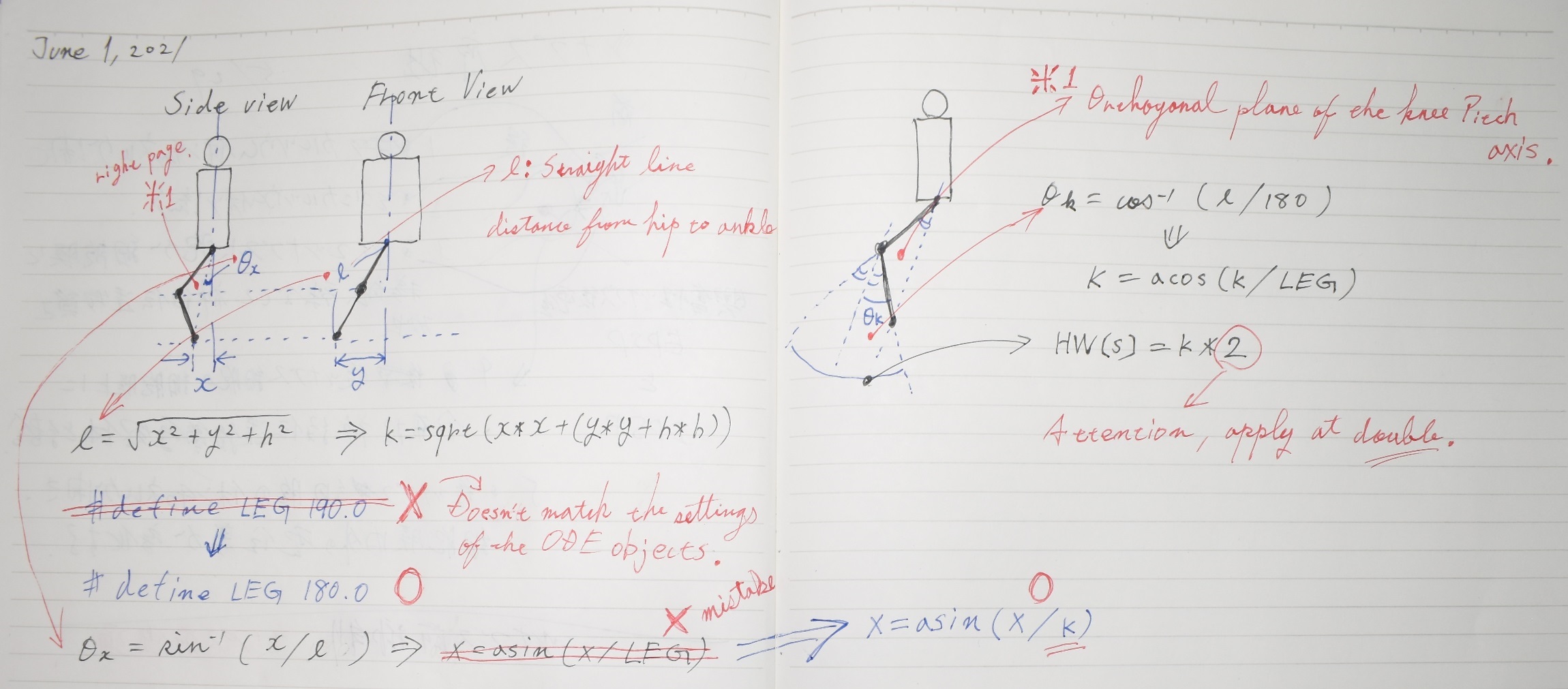
Q.3
It seems that K1W and K2W are both used for hip joint lateral writing (ÒÖß¡ûüp).
Was this done intentionally? If so, would you be willing to explain the purpose of that to us?
A.3
K2W is for hip yaw axis and is not used in this simulation.
I deleted it so that there is no misunderstanding.
Updated core.h and biped.cpp.
Q.4
Wefve observed that dxi and dyi are used frequently in the UVC section of your code. Even after thorough investigation, we were unable to figure out what specifically these variables represent. Is this something you would be able to show us?
A.4
dxi is equivalent to I in PID control,
and is for converting the tilt angle in the pitch direction into the distance in the front-back direction and integrating it.
By superimposing dxi on the stride length,
the front-back direction of the upper body is kept vertical.
dyi has the same idea as dxi, and keeps it vertical with respect to the lateral direction of the upper body.
The basic idea of UVC is to superimpose the inclination of the upper body on the hip joint angle and keep the upper body vertical at all times.
In this simulation, the same effect is obtained by converting the tilt angle into the stride for convenience.
Q.5
Your code heavily relies on the alternation between support leg and free leg. Many variables are arrays of 2 that house only 0 and 1. In some instances, 0 indicates support leg and 1 indicates the free leg. However, we are not sure if that is the case for all variables of this type, and we theorize that some of them indicate the left and right legs. Is this assumption correct?
A.5
jikuasi is a Japanese translation of the pivot foot and represents the foot on the grounded side.
When jikuasi is 0, the right foot is in contact with the ground, and when it is 1,
the left foot is in contact with the ground.
Q.6
In this video when the hand pushes the robot (in the experiment), how does this trigger the movement in the code?
A.6
In the actual machine, the walking motion is started when a certain inclination is detected,
and when the walking speed exceeds a certain speed, the walking speed is maintained.
These are convenient means only for the actual machine and are not implemented in the ODE simulation software.
UVC can be used not only for maintaining balance,
but also for various applications such as walking start control and constant-velocity walking.
Q.7
You are using head angular movement and rotation,to adjust movement of the body.
Rot = dBodyGetRotation(HEADT.b);
fbRad = asin(Rot[8]);
lrRad = asin(Rot[9]);
Rot = dBodyGetAngularVel(HEADT.b);
fbAV = Rot[1];
lrAV = Rot[0];
What if make invisible sphere (or 2 invisible circles) with the center in loin,
and use it as calculation parameter for torso movement?
A.7
fbAV and lrAV are used in the footCont(float x,float y,float h,int s) function,
but they are currently disabled.
In other words, at present, only the angle(fbRad and lrRad) is valid,
so even if you measure the angle with a sphere centered on the waist or calculate with the current head object,
the behavior of the robot will not change.
Q.8
You mention dxi is like the integral (I) term in PID. In my own code, I have renamed dxi to I_pitch and dyi to I_roll (relative to the hip). Would this be correct?
A.8
It is correct. For programming reasons, I control the robot's stride to keep its upper body vertical, but in principle it is more direct and easier to evaluate by superimposing deviations on the pitch angle and roll angle as you did. I think.
Q.9
Are you considering a proportional term or differential term?
A.9
UVC does not try to maintain any equilibrium point like the general PID control target, but merely keeps the upper body vertical. Therefore, in UVC, using the differential term or proportional term may be rather unstable. In my past productions, tightrope walking robots, all the terms of PID (maintaining the equilibrium point) are applied.
Q.10
You mention: "By superimposing dxi on the stride length, the front-back direction of the upper body is kept vertical. " Would you be able to clarify what you mean by this?
A.10
The current calculation method may have been too rough for how to keep the upper body angle vertical by controlling the stride length. For the time being, it worked, so it remains as it is, but it is a considerable omission. As mentioned above, the method of superimposing the deviation of the upper body angle on the pitch angle and roll angle of the supporting leg hip joint is a little complicated, but I think that better results can be obtained.
Q.11
Are you essentially trying to cancel out the angle of the upper body relative the waist by producing joint angles in "the opposite direction"?
A.11
That's right. The basis of UVC is to superimpose (integrate) the inclination (deviation) of the upper body with respect to the vertical on the hip joint angle and try to rebuild the upper body vertically.
Q.12
Would you be able to tell me how you determined values for certain variables? In particular, I am a bit uncertain about where to get the following variables for our robot: -autoH -autoHs -adjFr
A.12
autoHs is a variable that stores the maximum length from the robot's hip to ankle. (Maximum length is 180) autoHs is a variable that stores the standard length from the robot's hip to ankle. (Standard length is 170) The standard length is slightly shorter than the maximum length so that the knee is slightly bent so that no singularity occurs when the swing leg touches the ground. Also, when the robot is started, the knees are slowly bent by subtracting autoHs little by little to gently shift to the idle state. adjFr is for storing the value to correct the position of the center of gravity of the robot that is slightly shifted forward in the idle state.
Q.13
I am assuming fh and fhMax stands for foot height, but I am not certain
A.13
fh is a variable that represents the height of the foot and is a sine curve. The peak value of the sine curve is fhMax.
Q.14
Additionally, would you mind explaining where you got these values (or weights) in UVC: 1.5, 193, 1.5, 130?
k = 1.5 * 193 * sin(lrRad); //// Left-right displacement ////
k = 1.5 * 130 * sin(fbRad); //// Forward-backward displacement ////
A.14
1.5 is the value obtained experimentally (generally the optimum value). It doesn't make much sense to explain the background of 193 and 130, and when 1.5 * 193=289.5 and 1.5*130=195 are set as the coefficients, the movement becomes relatively stable.
Q.15
Please let me know if I can clarify anything. If there are any issues, please let me know.
A.15
The sample code is just one example of how UVC works, it's not optimized and it's very rough. So it may not make much sense to dig into the details. Rather, I hope that you will understand the basic concept of UVC, and based on that, you will be able to try out your own ideas and take on the challenge of applying it to actual machines.